743 Cgates
743 : Cgates
- Author: Tommy Thorn
- Description: Testing two different Cgate implementations and rings
- GitHub repository
- Open in 3D viewer
- Clock: 0 Hz
How it works
(This is a variant of tt06-ncl-lfsr, but with different C-gate implementations)
Muller's C-gate is a state-holding element with two inputs A and B, and an output Q. Q holds the previous state unless A == B in which case it takes on this value. There are many ways to implement the C-gate. In this design, we try two: building it from a latch and building it out of combinatorial logic. The two inputs ui[0] and ui[1] are fed to two C-gates Cl and Cc, build with a latch and combinatorial logic respectively. Their respective outputs are wired to uo[0] and uo[1].
We also build four rings from this, with uo[2] and uo[3] being the output of a four stage build from Cl and Cc gates respectively. Similar for uo[4]/uo[5] except using 16 stage rings and uo[6]/uo[7] for 64 stage rings.
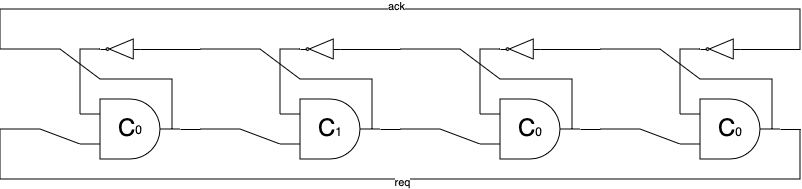
Since the pulse from each C-gate rings last only a few gate delay times, we use it to feed a toggle flip-flop, thus the corresponding output ping will toggle every time the pulse makes it round the ring. In other words, the cycle time of 4, 16, and 64 stage ring corresponding 8, 32, and 128 times the average stage delay of the corresponding ring.
Why is this interesting? Most asynchronous circuits disciplines rely heavily on the Cgate and this stage delay represents the absolute best-case for an asynchronous pipestage. Of course, for most interesting circuits the stage delay will be dominated by the computation performed.
How to test
Set ui[0] and ui[1] different values and verify that uo[0]/uo[1] only changes when both agree. The remaining six uo outputs corresponding to six rings, two 4-stage, two 16-stage, and two 64-stage. The first of each pair are built from latches, the latter from combinatorial logic. It will be interesting to see which is faster. The outputs are limited to 33 MHz / 30.3 ns, thus if the stage delay is less 3.8 ns we likely will not observe anything. For the other two the limits, are 947 ps and 237 ps, respectively. In hindsight, I should have made the rings more than an order of magnitude longer.
External hardware
For the basic test the rp2040 on the bringup board should be enough for the ring test, an oscilloscope is definely required to see anything from the rings.
IO
| # | Input | Output | Bidirectional |
|---|---|---|---|
| 0 | A | Ql | |
| 1 | B | Qc | |
| 2 | R4l | ||
| 3 | R4c | ||
| 4 | R16l | ||
| 5 | R16c | ||
| 6 | RTBDl | ||
| 7 | RTBDc |