258 Array multiplier :: Quicker, easier and cheaper to make your own chip!

alt text

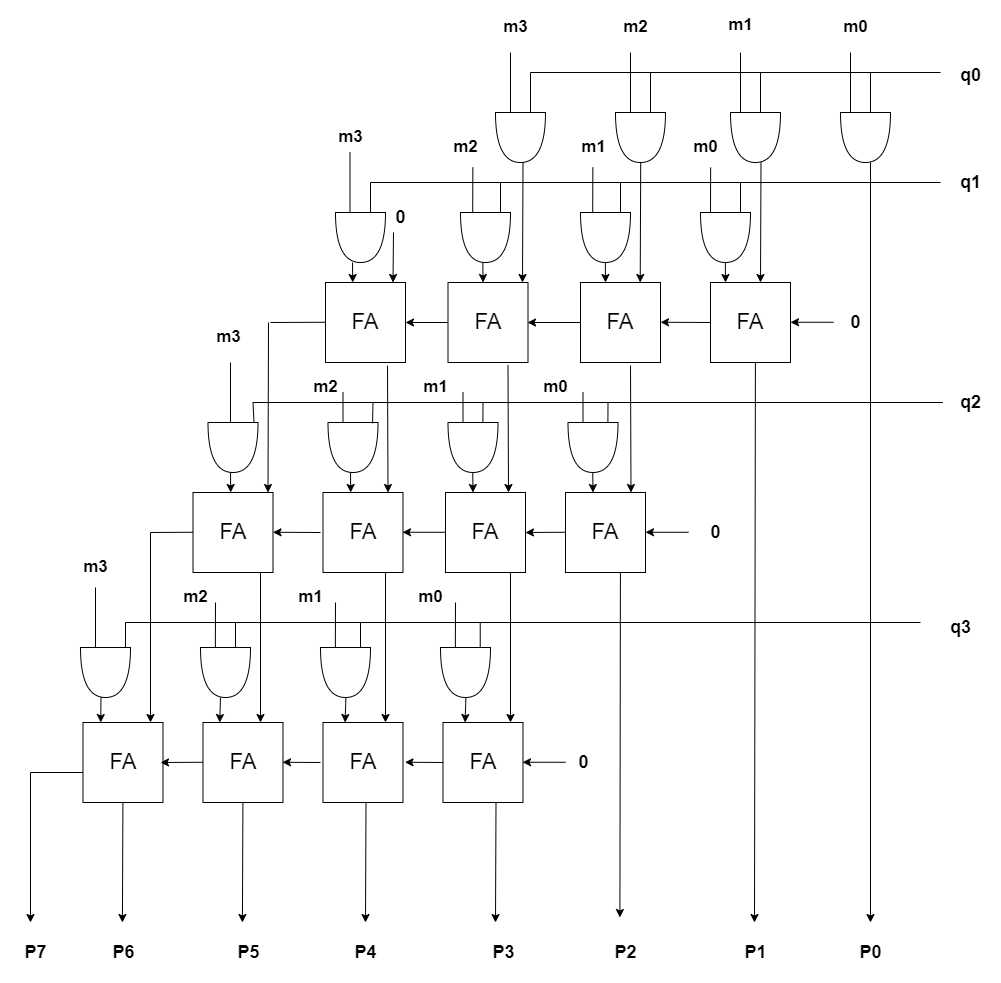
How it works

When multiplying two 4-bit numbers, m = 1011 (11 in decimal) and q = 1101 (13 in decimal), the multiplier first generates partial products (m0, m1, m2, and m3) by AND-ing each bit of q with all bits of m. For instance, m0 results from q[0] & m, producing 1101, and similarly, m2 and m3 are also 1101, while m1 is 0000 since q[1] is zero. These partial products are then summed column-wise using full adders, combining overlapping bits and propagating carries. For example, in the first column, p[0] is directly assigned from m0[0], which is 1. Moving to the second column, we add m0[1] and m1[0] with any carry (which is zero in this case), giving a sum of 1 and a carry of zero, resulting in p[1] = 1. In the third column, adding m0[2], m1[1], and the carry results in a sum of 0 and a carry of zero, making p[2] = 0. In the fourth column, adding m0[3] and m1[2] with zero carry gives a sum of 1 and no carry, so p[3] = 1. Continuing this process for all columns and partial products, the final 8-bit product p is formed as 10011111 (143 in decimal), representing the correct product of 11 and 13.

How to test

The Cocotb testbench for your project sets up a clock running at 100 KHz and initializes the design by asserting and de-asserting a reset signal (rst_n). It tests our Verilog module by setting various input values (ui_in, uio_in) and checking the resulting output (uo_out) using assertions to ensure correctness. For each test case, like Test Case 3, the test sets specific input values (e.g., 0x2_6), waits for one clock cycle to allow the inputs to propagate through the design, and verifies that the output matches an expected value (in this case, 12). This structured approach allows us to efficiently validate the behavior of our module for different input scenarios and edge cases.

External hardware

N/A List external hardware used in your project (e.g. PMOD, LED display, etc), if any

#	Input	Output
0	q[0]	p[0]
1	q[1]	p[1]
2	q[2]	p[2]
3	q[3]	p[3]
4	m[0]	p[4]
5	m[1]	p[5]
6	m[2]	p[6]
7	m[3]	p[7]

258 Array multiplier