104 4-spin Ising Chain Simulation
104 : 0b 001 101 000 : 4-spin Ising Chain Simulation
- Author: Seppe Van Dyck
- Description: A self-contained physics simulation. This circuit simulates 4 spins of an Ising chain in an external field.
- GitHub repository
- Wokwi project
- Extra docs
- Clock: 20 Hz
- External hardware: None
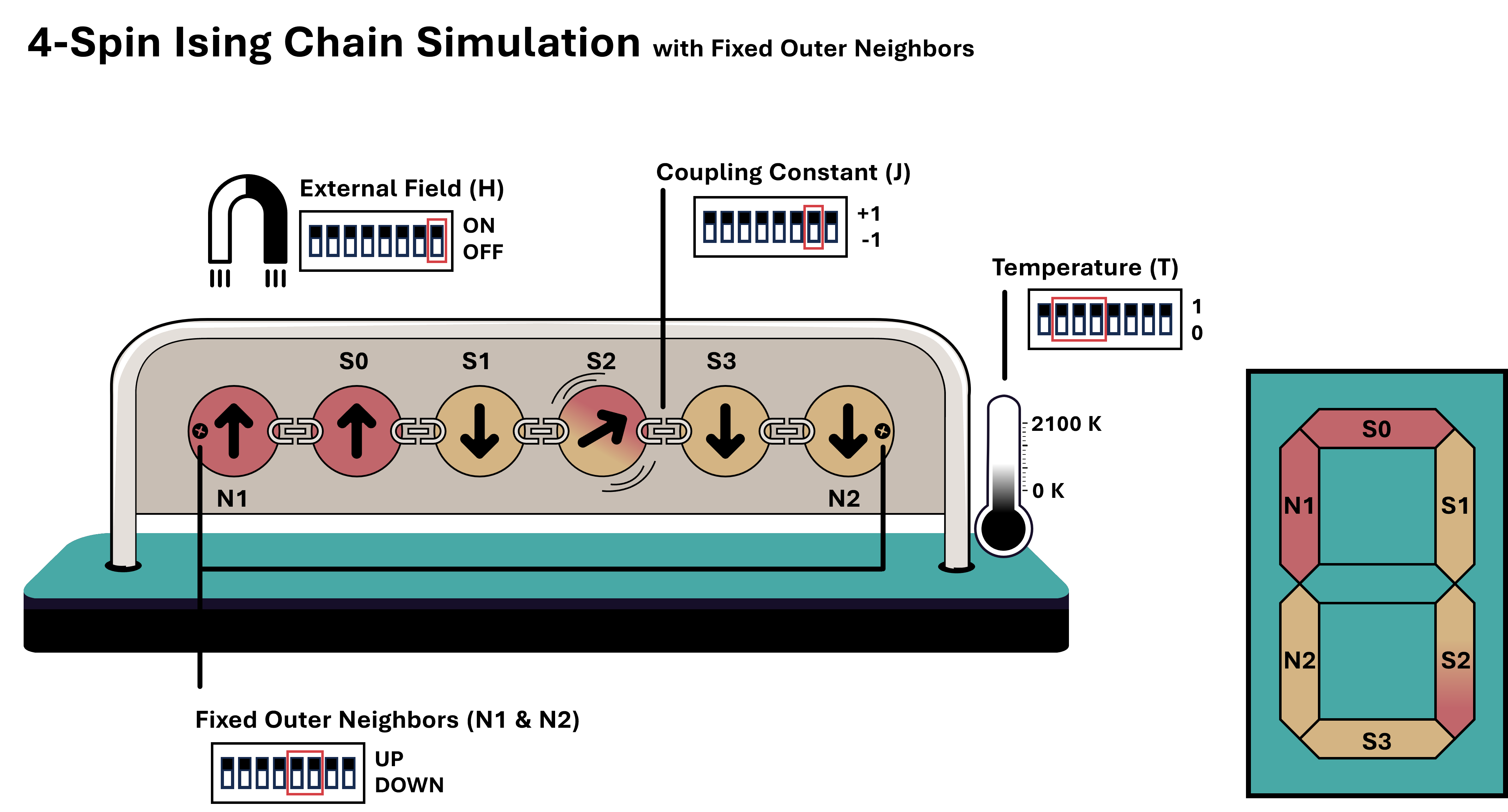
How it works
It runs the Metropolis-Hastings monte-carlo algorithm to simulate 4 Ising spins in a linear chain with two external neighbours and an external field. Every monte-carlo step (10 clock cycles) a random number is created through a 32-bit LFSR and is compared to an 8-bit representations of the acceptance probability of a random spin flip. Using the inputs for external neighbors, N of these circuits can be chained together to create a 4N spin Ising chain.
How to test
The design can be tested by enabling one of the neighbours (input 4 or 5) and leave all other inputs low, the system will evolve into a ground state with every other spin pointing up.
IO
| # | Input | Output |
|---|---|---|
| 0 | clock, clock input. | segment a, Spin 0. |
| 1 | T0, LSB of the 3-bit temperature representation. | segment b, Spin 1. |
| 2 | T1, Middle bit of the 3-bit temperature. | segment c, Spin 2. |
| 3 | T2, MSB of the 3-bit temperature. | segment d, Spin 3. |
| 4 | N1, Value of neighbour 1 (up/1 or down/0). | segment e, Neighbour 2. |
| 5 | N2, Value of neighbour 2 (up/1 or down/0). | segment f, Neighbour 1. |
| 6 | J, The sign of the NN coupling constant J. | none |
| 7 | H, Value of the coupling to the external field H. | segment h, MC Step Indicator. |